ELBOの計算とモデル選択
はじめに
ベイズ推論におけるモデル選択はどのように行えばいいのか実験しました。 一例にすぎませんが...
モデル
2次元の混合ガウス分布を変分推論によって学習します。観測データx_nがクラスターkの2次元ガウス分布から生成されているとします。 x_nがどのクラスターに属するかを表す潜在変数s_nを用いると生成モデルは次のように表すことができます。

ガウス分布の平均および精度パラメータに対しては、ガウス・ウィシャート分布を事前分布として与えます。

潜在変数は、カテゴリ分布で表します。

カテゴリ分布のパラメータに対しては、ディリクレ分布を事前分布として与えます。

ELBO
変分推論による学習は、周辺尤度の下限を最大化することと同じです。具体的には、周辺尤度の対数に対してイェンセンの不等式を用いることで 得られる下限、ELBO; evidence lower boundを最大化します。 したがって、モデルが観測データをどれくらい説明できているかはこのELBOが一つの評価基準になると言えるでしょう。

上式の期待値およびKLダイバージェンスの計算は参考文献を参照するといいと思います。
実験
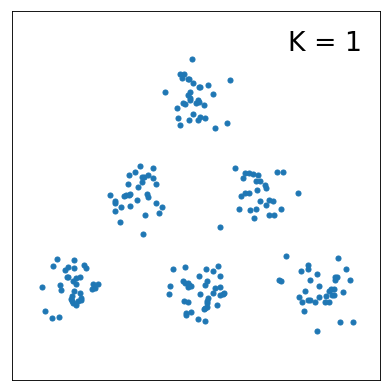
サンプルデータを下に示しました。一見して分かる通り、クラスター数はK=6です。

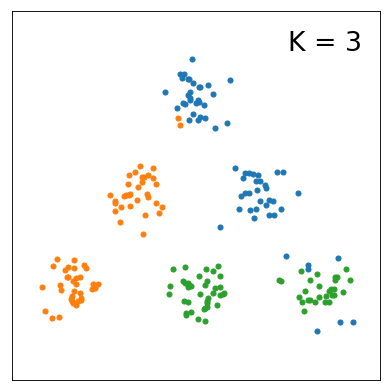
今回の実験の目的は、モデルのクラスター数に対してELBOの値がどのように変化するのかを知ることです。 まず、K=1~10まで変えたときの分布の変化を以下にまとめました。
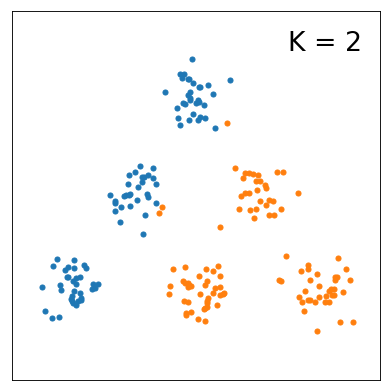


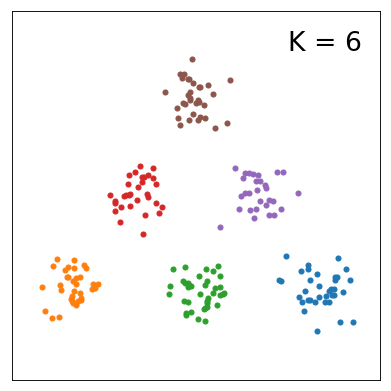
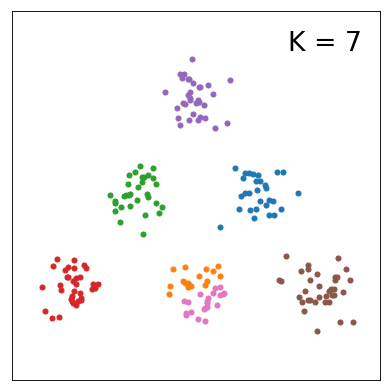
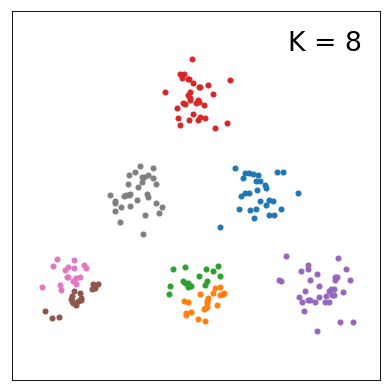
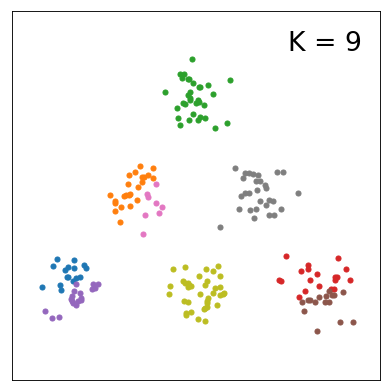

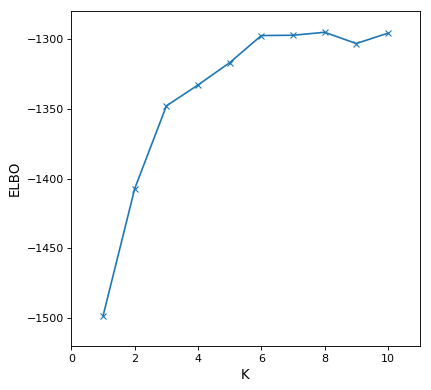
各学習結果のELBOをプロットすると下図の通りです。K=6以上になると、ELBOがほとんど変わらないことが分かりました。サンプルデータを説明する上では、K=6として十分であると解釈できそうです。 あるいは、K>6としてもデータに対してパラメータが過剰であるという説明の仕方もできそうです。