混合ポアソン分布に対する隠れマルコフモデル

はじめに

この記事は以下の書籍の内容に依るところが大きいです。詳しい解説は以下の書籍をあたってください。

機械学習スタートアップシリーズ ベイズ推論による機械学習入門 (KS情報科学専門書)

モデル

この記事で扱うモデルは隠れマルコフモデルである。 時系列で得られるN個の観測データがポアソン分布に従うことを想定するとき、同時分布を次式のように表す。

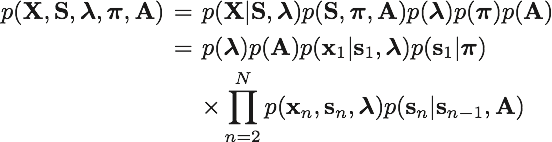
ここで、Xは観測データ、Sは潜在変数、{λ,π,A}はパラメータである。

観測モデルはポアソン分布を用いて次のように表す。

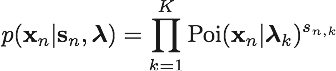
ここで、クラスタの総数をKとした。ポアソン分布のパラメータλはガンマ分布に従うとして、次式で表す。

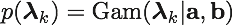
ここで、aおよびbはハイパーパラメータである。

初期状態s_1は、次式のカテゴリ分布で決定される。

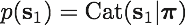
また、パラメータπは次式のディリクレ分布に従うとする。

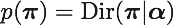
ここで、αはハイパーパラメータである。

状態s_n-1からs_nへの遷移は次式のように表す。

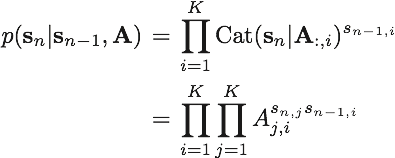
ここで、A_jiはクラスタiからクラスタjへの遷移確率を表す。また、A_:,iは次式のディリクレ分布に従うとする。

ここで、βはハイパーパラメータである。

変分推論

ここからは、実際に観測データから状態を推論するアルゴリズムを考える。この記事では変分推論を用いる。 特に、潜在変数が時間方向に独立であることを仮定した推論方法を扱う(完全分解変分推論)。 変分推論では、変数およびパラメータの事後分布を次式のような分布で近似する。

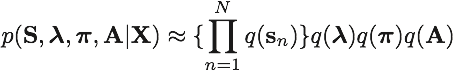
式の導出過程を省くと、最終的に得られる近似事後分布は以下の通りとなる。まず、パラメータλの事後分布は

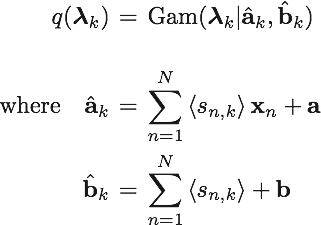
となる。次に、パラメータπの事後分布は

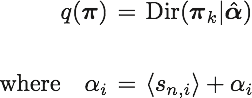
となる。パラメータAの事後分布は

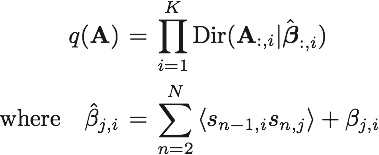
となる。最後に、潜在変数の事後分布をまとめる。s_1は

となる。s_n(1<n<N)は

となる。s_Nは

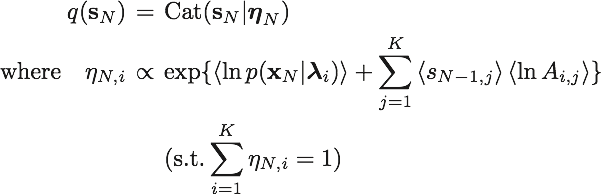
となる。

実験

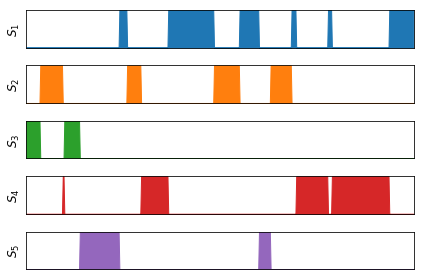
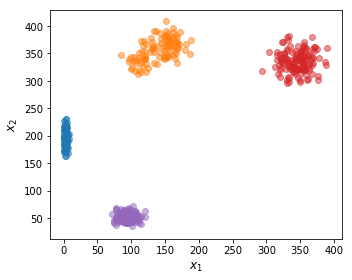
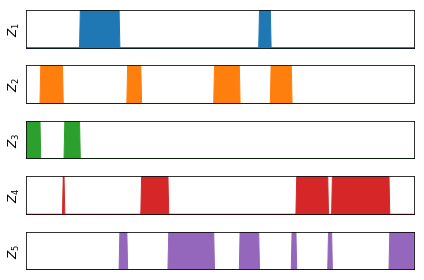
では、実際にデータを使った推論を試してみる。観測データの次元数を2次元、クラスタの総数をK=5、サンプル数をN=500としてデータを生成した。 2次元平面上にプロットした観測データと横軸を時間軸とした潜在変数の分布を下図に示す。

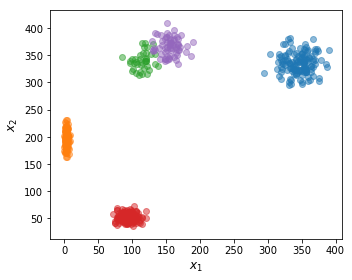
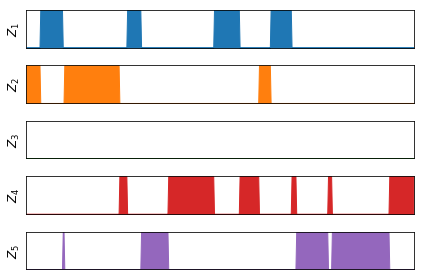
推論結果を下図に示す。

試行1回目

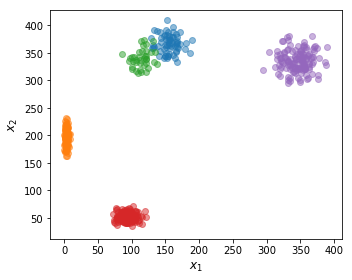
試行2回目

推論結果の妥当性を調べるにはELBOを計算する必要がある。

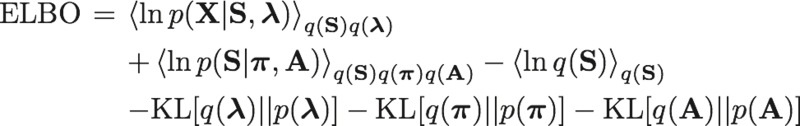
最後に

Githubにjupyter notebookを公開(2018/04/07, "update_Z"を修正) github.com